Linear Quadratic Regulator (LQR) 설명 및 구현

26 November 2020 - 6 mins read time
Tags: optimal control

Background

Optimization Problem

• LQR은 최적화 문제의 대표적인 사례이다. 최적화 문제는 아래와 같이 수식화할 수 있다.

• \[\underset{x}{minimize}f(x) \\ s.t. \quad g_i(x)\leq 0, \forall i, \\ h_j(x) = 0, \forall j.\]
• 위에서 $f(x)$는 objective function이라 부른다.

Optimality Condition

• KKT conditions은 Nonconvex problem의 경우, optimality를 위한 필요조건이고, convex problem의 경우, optimality를 위한 필요충분조건이다.

• LQR의 경우, 모든 변수에 대해 opjective가 quadratic 하므로 convex 하다. 따라서 KKT condtions을 통해 구한 control이 optimal함을 만족한다.

• 아래 챕터에서 KKT condtions을 통해 control 계산을 유도할 것이다.

• Lagrangian function : $L(x, \mu, \lambda) := f(x) + \mu^Tg(x) + \lambda^Th(x)$

• KKT condition :

  1. \[\frac{\partial L(x, \mu, \lambda)}{\partial x} = 0\]
  2. \[g_i(x)\leq 0, \forall i,\;\; h_j(x) = 0, \forall j\]
  3. \[\mu_i \geq 0, \forall i\]
  4. \[\mu_i g_i(x) = 0, \forall i\]

LQR for Discrete Time & Finite Horizon

Problem Setting

• $x_{\mathrm{des}} = 0, u_{\mathrm{des}} = 0$ 인 경우, 아래와 같이 문제를 정의할 수 있다.

• \[\underset{x_{0,1,...,N}, u_{0,1,...,N-1}}{minimize} \frac{1}{2}x_{N}^{T}Q_{f}x_{N} + \sum_{i=0}^{N-1}\left[\frac{1}{2}x_{i}^{T}Qx_{i} + \frac{1}{2}u_{i}^{T}Ru_{i} \right] \\ s.t. \quad x_{i+1} = Ax_i + Bu_i, \; i = 0,1,...,N-1, \\ x_0 =x_{\mathrm{init}}.\]
• 만일 $x_{\mathrm{des}} \neq 0$ 또는 $u_{\mathrm{des}} \neq 0$ 인 경우라 하더라도, $x = \hat{x} - \hat{x}_{\mathrm{des}}$, $u = \hat{u} - \hat{u}_{\mathrm{des}}$ ($\hat{x}, \hat{u}$ 이 실제 state 및 input) 으로 치환하면 위의 식을 통해 control을 구할 수 있다.

Lagrangian Function 및 Hamiltonian Matrix

• Lagrangian function : $L(x, u, \lambda) := \frac{1}{2}x_{N}^{T}Q_{f}x_{N} + \sum_{i=0}^{N-1}\left[\frac{1}{2}x_{i}^{T}Qx_{i} + \frac{1}{2}u_{i}^{T}Ru_{i} + \lambda_i \cdot (Ax_i + Bu_i - x_{i+1}) \right]$

• Hamiltonian matrix : $H(x_i, u_i, \lambda_i) := \frac{1}{2}x_{i}^{T}Qx_{i} + \frac{1}{2}u_{i}^{T}Ru_{i} + \lambda_i \cdot (Ax_i + Bu_i)$

• Hamiltonian을 이용해 Larangian을 다시 표현하면 아래와 같다.

• \[\begin{aligned} L(x, u, \lambda) &= \frac{1}{2}x_{N}^{T}Q_{f}x_{N} + \sum_{i=0}^{N-1}\left[H(x_i, u_i, \lambda_i) - \lambda_{i}x_{i+1} \right] \\ &= \frac{1}{2}x_{N}^{T}Q_{f}x_{N} - \lambda_{N-1}x_{N} + H(x_0, u_0, \lambda_0) + \sum_{i=1}^{N-1}\left[H(x_i, u_i, \lambda_i) - \lambda_{i-1}x_{i} \right] \\ \end{aligned}\]

• 위의 식으로부터 KKT conditions 중 첫 번째 조건인, 1차 미분값을 0으로 하는 조건을 사용하면 아래와 같은 식을 얻을 수 있다. 이때 $x_{0,1,…N}, u_{0,1,…,N-1}$ 에 대해 모두 미분 값이 0이어야 한다.

  1. stationarity :
     • \[\frac{\partial L}{\partial x_N} = Q_fx_N - \lambda_{N-1} = 0, \\ \frac{\partial L}{\partial x_i} = \frac{\partial H}{\partial x_i} - \lambda_{i-1} = 0, \;\; i=1,2,..,N-1, \\ \frac{\partial L}{\partial u_i} = \frac{\partial H}{\partial u_i} = 0, \;\; i=0,1,..,N-1. \\\]
  2. primal feasibility :
     • \[x_0 = x_{\mathrm{init}}, \\ x_{i+1} = Ax_i + Bu_i, \; i = 0,1,...,N-1. \\\]

• LQR의 경우, equality constraints뿐이므로, dual feasibility 나 complementary slackness 조건은 생략할 수 있다.

• 다음 챕터에서는 위에서 얻은 식들을 이용해 optimal control을 계산할 것이다.

Optimal Control Derivation

• stationary condition을 이용해 아래와 같은 식을 쓸 수 있다.

• \[\lambda_{N-1} = Q_f x_N, \\ Qx_{i} + A^T\lambda_i = \lambda_{i-1}, \;\; i=1,2,..,N-1, \\ u_i = - R^{-1}B^T\lambda_{i}, \;\; i=0,1,..,N-1. \\\]

• 먼저 $u_{N-1}$을 구해볼 수 있다.

• \[\begin{aligned} u_{N-1} &= -R^{-1}B^T\lambda_{N-1} \\ &= -R^{-1}B^TQ_f^T x_N \\ &= -R^{-1}B^TQ_f (Ax_{N-1} + Bu_{N-1}). \\ u_{N-1} &= -(I + R^{-1}B^TQ_fB)^{-1}R^{-1}B^TQ_fAx_{N-1} \\ &= -(R + B^TQ_fB)^{-1}B^TQ_fAx_{N-1} \\ &:= -P_{N-1}x_{N-1}. \\ \end{aligned}\]

• 위 식을 통해 $u_{N-1}$을 $x_{N-1}$에 대해 구할 수 있었다 ($P_{N-1} := (R + B^TQ_fB)^{-1}B^TQ_fA$). 이를 바탕으로 $\lambda_{N-2}$ 또한 아래와 같이 구할 수 있다.

• \[\begin{aligned} \lambda_{N-2} &= Qx_{N-1} + A^T\lambda_{N-1} \\ &= Qx_{N-1} + A^TQ_fx_N \\ &= Qx_{N-1} + A^TQ_f(Ax_{N-1} + Bu_{N-1}) \\ &= Qx_{N-1} + A^TQ_f(Ax_{N-1} - BP_{N-1}x_{N-1}) \\ &= (Q + A^TQ_f(A - BP_{N-1}))x_{N-1} \\ &:= S_{N-1}x_{N-1} \\ \end{aligned}\]

• 위 식을 통해 $\lambda_{N-2}$ 또한 $x_{N-1}$로 표현할 수 있다 ($S_{N-1} = Q + A^TQ_f(A - BP_{N-1})$). $\lambda_{N-1} = Q_fx_N$ 이었으므로, $S_N=Q_f$라 볼 수 있고, 이로부터 재귀적으로 $u_i = -P_ix_i$를 아래와 같이 구할 수 있다.

• \[P_i = (R + B^TS_{i+1}B)^{-1}B^TS_{i+1}A, \;\; i=0,1,...,N-1. \\ S_i = Q + A^TS_{i+1}(A - BP_{i}), \;\; i=0,1,...,N-1. \\\]

Optimal Control Derivation via Dynamic Programming

위에서는 optimization problem 접근 방식으로 control을 구하였다. 이와 다른 방식으로, Reinforcement Learning (그 중에서 value iteration 방식)과 같이 각 state 마다 value function을 정의하여 control을 구할 수도 있다. 이러한 value function을 cost-to-go 함수라 말한다. 이 방식을 통해 유도한 결과 또한 위와 동일한 결과를 얻을 수 있다. 이번 포스트에서는 유도를 생략하고 다음 기회에 해볼 예정이다.

Code Implemetation

LQR과 같은 optimal controller들은 계산량이 많아 파이썬에서 구현하면 real-time control이 어려워진다. 이를 위해 LQR의 핵심 파트 ($P_i$ matrix를 구하는 계산) 만 c++로 작성 및 동적 라이브러리 파일을 compile한 뒤, 파이썬으로 모듈화 하였다. c++ 코드는 아래와 같다.

void get_action(int X_DIM, int U_DIM, double* init_x, int time_horizon, double* A_data, double* B_data,
                    double* R_data, double* Q_data, double* Qf_data, double* return_var){
    // ######## declare variables ########
    mat A_mat(A_data, X_DIM, X_DIM);
    mat B_mat(B_data, X_DIM, U_DIM);
    mat R_mat(R_data, U_DIM, U_DIM);
    mat Q_mat(Q_data, X_DIM, X_DIM);
    mat Qf_mat(Qf_data, X_DIM, X_DIM);

    mat* P_mat_list = new mat[time_horizon];
    mat S_mat = Qf_mat;
    // ###################################

    for(int t_idx=time_horizon-1; t_idx>=0; t_idx--){
        P_mat_list[t_idx] = (R_mat + B_mat.transpose().matmul(S_mat.matmul(B_mat))).inverse_matmul(B_mat.transpose().matmul(S_mat.matmul(A_mat)));
        S_mat = Q_mat + A_mat.transpose().matmul(S_mat.matmul(A_mat - B_mat.matmul(P_mat_list[t_idx])));
    }

    for(int i=0;i<time_horizon;i++){
        memcpy(&return_var[i*X_DIM*U_DIM], P_mat_list[i].data, sizeof(double)*X_DIM*U_DIM);
    }

    delete[] P_mat_list;
    return;
    }

컴파일 과정, 모듈화 과정, 파이썬 코드는 모두 여기에 소개되어 있다.

Result

• Openai Gym의 cartpole 환경을 사용하였으며, input을 x방향 force로 변형하였다.

• 

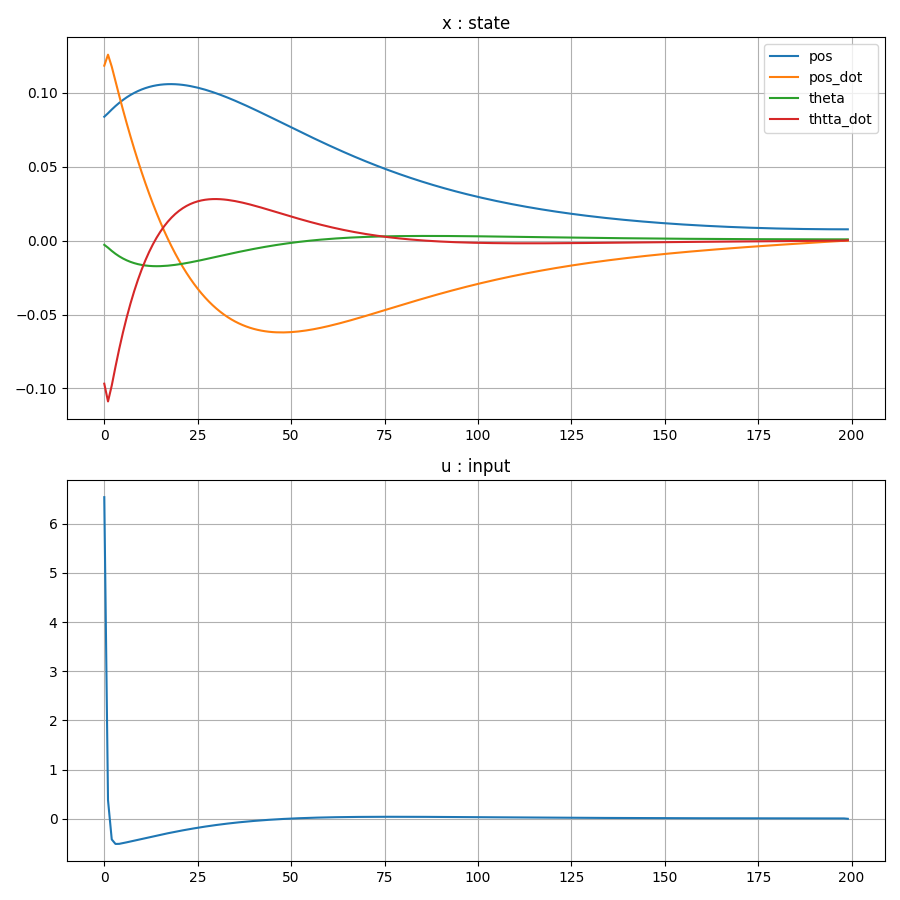
Conclusion

optimal control의 가장 기본이 되는 방법인 LQR을 다뤄보았다. 다음번엔, non linear dynamics에서 적용가능한 iterative LQR (iLQR)에 대해 다룰 예정이다.